
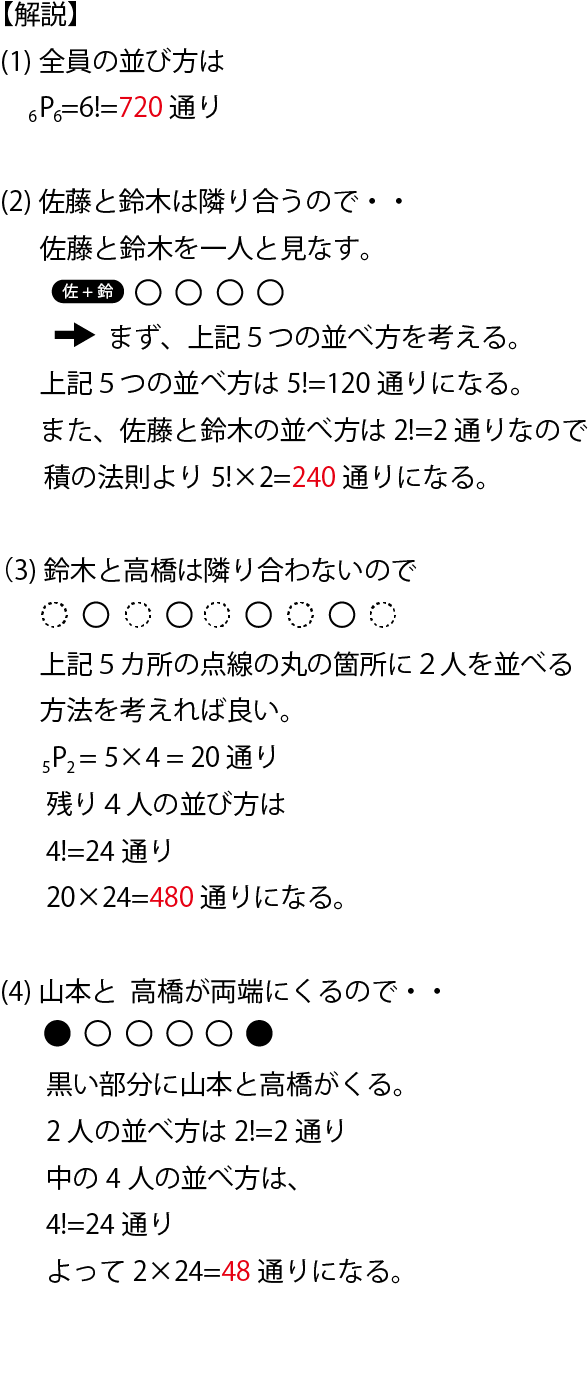
高校数学 数a 14 組み合わせ 基本編 Youtube
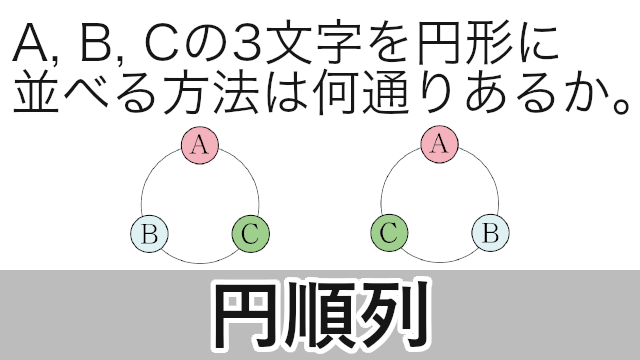
次は順番を振らない円順列と、隣り合わせの順列の融合問題です。 基本的には両方の気をつけるべきポイントを抑えれば難なく解けます。 まず順番を振らない円順列の場合、 一人を固定すれば良い のでしたね。 先程同様にAを固定します。 次に 3!(通り)が今回は1(通り)と数えられるので、 (n1)通りと3!(通り)が対応します。 まとめると、 #1を解いて、6n=732⇔n=122(通り)// 例題(22)6人を区別のつかない3部屋に分ける場合の数を求めよ。但し空室があってはならないとする。
数学 何通りあるかをもとめる
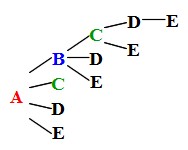
数学 何通りあるかをもとめる- ここでの内容は、こんな人に向けて書いています 中学の確率の求め方がわからない 確率の公式を知りたい 公式を使った問題の解き方を知りたい 中学校の確率の問題は、基本的にはたった一つの公式を覚えるだけです。 逆に言うと、この公式を覚えて使いこなすことができないと、確率の問 数学について 硬貨の一部または全部をつかって支払うことができる金額は何通りか (1)10円4枚、50円1枚、100円3枚 (2)〃2枚、〃3枚、〃3枚 (3)〃7枚、〃1枚、〃3枚 という問題の解説をお願いします。 補足 解答をみると (1)39通り (2)29通り (3)42
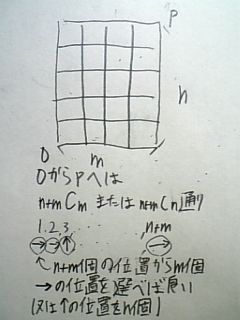
Math たて横の道路の道順 最も短い道のり を求める問題 働きアリ
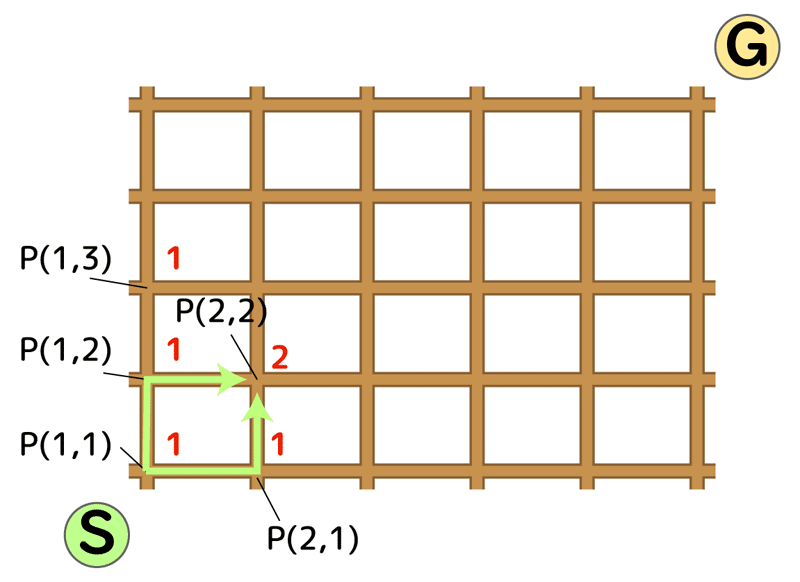
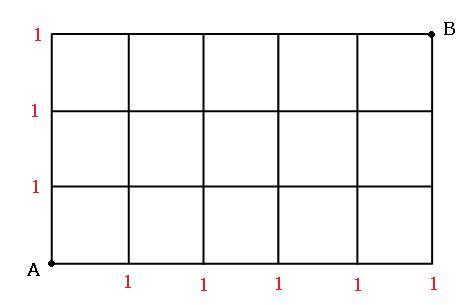
「田」 の端から端まで \\(6\\) 通り! 準備として, 「順列・組合せ」 について理解しておきましょう 最短経路数 って? 主に格子状の図形の線上を通り, 図形上の \\(2\\) 点を遠回りせずに結ぶ場合の数 麻雀の数学 0438 確率」の計算結果と一致しており、全組合せのパターン数 は、「配牌の形は何通りあるか」で算出した値と一致していますので、双方のプログラムの計算結果が正しいことの確認にもなっています。 人を並べるときに「 が隣り合う」や「 が隣り合わない」という条件が付くことがあります。そのようなときに,毎回どうするのかと悩んでいては時間制限の厳しい試験では,完答できないときがあります。「 が隣り合う」ときたらこう考えるという軸とな
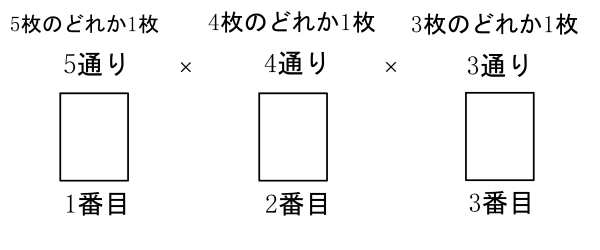
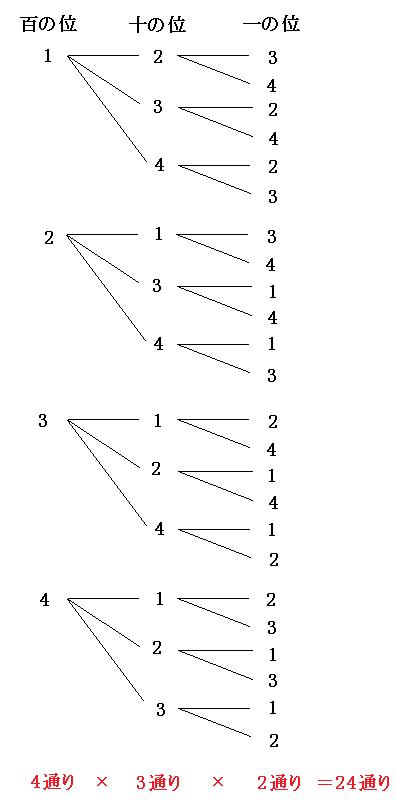
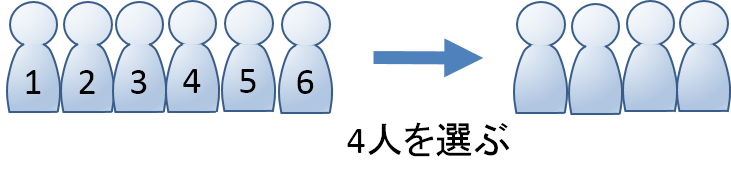
34,35,41,42,43,45,51,52,53,54)の通り これは、この順列の公式を使う事で 5 p 2 =5×4=通り と求めることができます。 下のように表にして考えると、順列が 5×4= になるのが分かりやすいです。 数学って難しい式をガリガリ計算していくイメージがあるかもしれません。 しかしこんな使い方もできるんですね! 是非、この話を飲み会の小ネタにしてみてはいかがでしょうか? 理系男子は合コンで話せば人気者になれるかも?笑 以上!数学雑学でし次のような街路において,A地点からB地点まで最短経路で行くとき,途中Q地点を通らずP地点を通る方法は何通りありますか 30 32 35 48 60 66 72 80 96 100 115 130 144
数学 何通りあるかをもとめるのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 何通りあるかをもとめる」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |
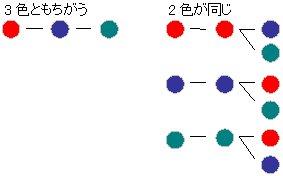
じゅず順列の問題の考え方 例 黒,赤,青,緑の4色の玉をじゅず状に並べるのは何通りか. じゅず順列では, 3 3 次元空間内の輪として同じものは同じ並べ方としてみます.つまり円順列において, 裏返して同じものは同じ並べ方とします . それを 組み合わせ C とは? 組み合わせとは、 人や物を選び出す/取り出すこと です。 選び出すだけなので、選び出す順番や、選び出したものの並び順は考慮しません。 組み合わせを意味する英単語「Combination」の頭文字をとって記号「\(\mathrm{C}\)」で表します。
Incoming Term: 数学 何通り 求め方, 数学 何通り, 数学 何通りあるかをもとめる, 数学 何通り 計算, 数学 何通り 円卓, 数学 何通りの行き方, 数学 何通り やり方,




0 件のコメント:
コメントを投稿